SIMCA Model Builder GUI
How to Assemble a SIMCA Model
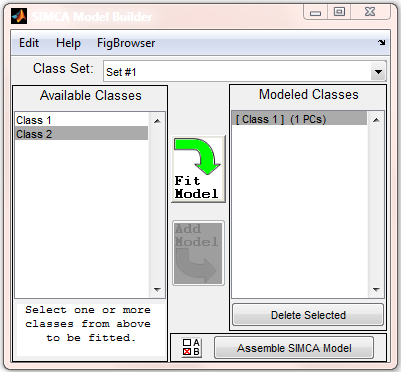
Working with the SIMCA Model Builder
In order to build a SIMCA model, SIMCA submodels must be built first. SIMCA submodels are essentially individual PCA models, each built on the data from a class or a group of classes. To build a submodel:
- If multiple class sets are available in the data, select a class set to model using the "Class Set" control at the top of the window (Note: all models must use the same class set. Changing the class set during model building will clear all existing submodels).
- Select one or more classes in the "Available Classes" list (Note: If multiple classes are selected for an individual submodel, all selected classes will be used in building the submodel).
- Click "Fit Model" to activate the PCA user interface in order to build a submodel.
- In the PCA interface, choose the appropriate preprocessing, number of components, validation settings etc. Note that the preprocessing and number of included variables may be set independently for each PCA submodel. See Review_Results_with_PLS_Toolbox.
- Once an acceptable submodel is constructed, return to the SIMCA interface and click "Add Model".
- Repeat the previous steps (2-5) for additional models.
- Adjust settings using the "SIMCA Model Options" button (The "A/B" button next to the "Assemble SIMCA Model" button). See 'Choosing the Classification rule' section below.
- Click "Assemble SIMCA Model".
- Review the assembled SIMCA model using the main Analysis window.
- To classify new data, import new data into the Analysis interface and click "Prediction" to apply the assembled SIMCA model.
Below is an image of the SIMCA Model Building interface after one class model has been built.
Choosing the Classification Rule
Within the SIMCA Model Options is the classification "Rule". There are four options:
- Q
- T^2
- Both
- Combined
The following discusses each rule.
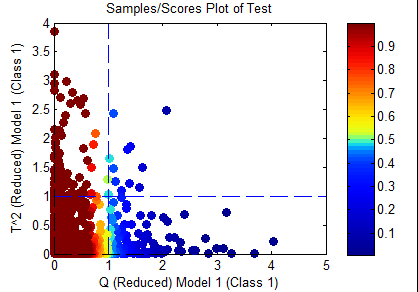
Q
Only samples which are inside the Q confidence limit specified in the options will be considered "in-class". This would include only the samples in yellow and red in the figure below.
This option is one historically used by many researchers as the Q statistic is often very sensitive to differences between species.
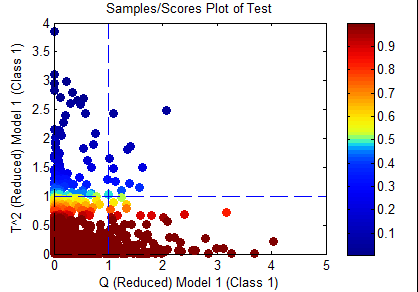
T^2
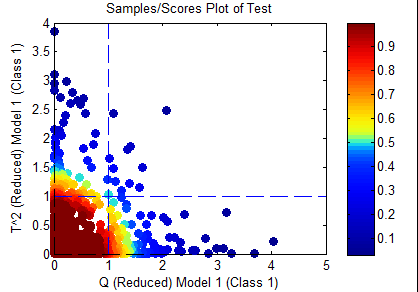
Only samples which are inside the T^2 confidence limit specified in the options will be considered "in-class". This would include only the samples in yellow and red in the figure below.
This option is an unusual option as it is often the Q residuals which best separate classes. However, in a case where the Q may drift (due to instrumentation variations or noise), the T^2 could be more diagnostic of class differences.
Both
Only samples which are inside both the T^2 and Q confidence limits specified in the options will be considered "in-class". This would include only the samples in yellow and red in the figure below.
Although this option is somewhat intuitive, it does ignore the concept that the within-class variation of two separate classes are not necessarily orthogonal and, thus, the "combined" rule may be more sensitive (see below.)
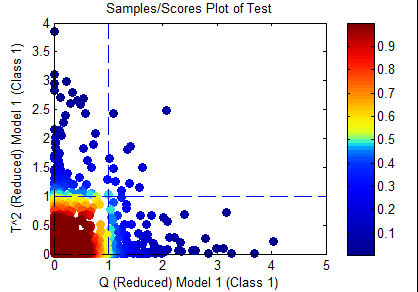
Combined
This rule first takes the Q and T^2 statistics "reduced" (normalized to) their confidence limits set in the options. Then the two statistics are combined using the equation:
- sqrt( Q^2 + (T^2)^2 )
Only samples inside the sqrt(2) limit will be considered "in-class". This would include only the samples in yellow and red in the figure below.
This option is quite useful because it allows differences in both T^2 and Q to be considered together. Although T^2 and Q are technically orthogonal statistics, the differences between classes are often not orthogonal but their class means are often different. Thus, a member of Class B would be expected to have both a projection into the model (indicated by the T^2) as well as residuals (indicated by the Q). Note that for a set of random data, this approach can be shown to reliably match the "true positive" rate expected for the given confidence limits.
See Also
simca, pca, analysis_GUI, T-Squared_Q_residuals_and_Contributions